Java集合框架之TreeMap详解

发表于 | 分类于 | 阅读量 次

本文基于jdk1.8介绍TreeMap。

TreeMap

在上一篇文章Java集合框架之LinkedHashMap详解中， 我们介绍了Java集合框架的一个类LinkedHashMap。今天我们来介绍一下java集合框架中的TreeMap，先回顾一下map接口的类图：

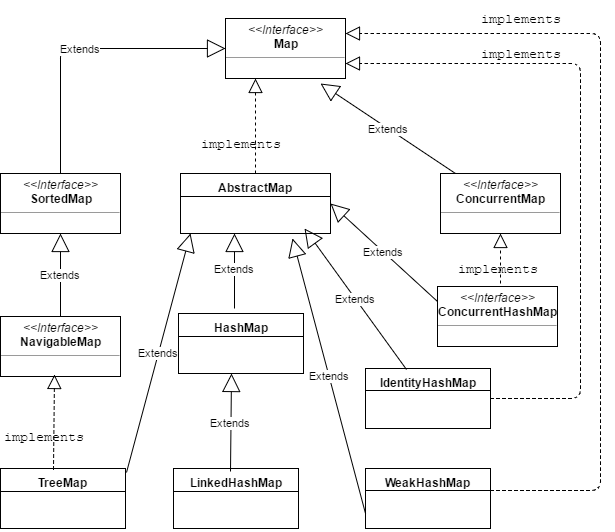
Map接口类图
Map接口类图

基本特性

从类图中我们可以看到，TreeMap继承自AbstractMap，并实现了NavigableMap、Cloneable和Serializable接口，AbstractMap完成了大部分map接口所支持的方法，而NavigableMap接口继承自SortedMap接口，SortedMap存储的是有序的键值对，他内部维护了一个Comparator比较器，NavigableMap是一个可导航的键-值对集合，具有了为给定搜索目标报告最接近匹配项的导航方法。所以可以总结TreeMap有以下特性：

1、排序性
2、可以被克隆
3、可以被序列化

与LinkedHashMap一样，TreeMap也保证了集合元素的顺序性，下面我们就来看一下它是如何实现顺序性的。

存储结构

分析一个数据类型最好的办法就是看它的内部存储结构，通过分析存储的数据结构，我们可以更清楚的看到它的实现原理和方法，从而更好的去使用，因为特定的数据结构只有用在特定的场景下，才会发挥它最大的作用。
TreeMap内部使用的数据结构为红黑树（Red-Black tree），关于红黑树，这里简单介绍一下，红黑树属于二叉排序树，但是在二叉排序树的基础上，又增加了一些规则，比如定义节点的着色等，这样就不会出现一些极端的情况，比如，整个树出现了偏离，变为了单分支结构的树，这样，整个树的高度就是n，n为全部的节点数。在这样的节点分部情况下，查找一个节点所需的时间复杂度为O(n)，为了避免这样的情况，聪明的人类又发明了另一种树形结构，叫做平衡二叉树，平衡二叉树查找、插入和删除在平均和最坏情况下的时间复杂度都是 O(logn)。红黑树就是平衡二叉树的一种实现方式。红黑树定义了一些规则，保证树的高度维持在logn。

1、每个结点要么是红的要么是黑的。
2、根结点是黑的。
3、每个叶结点（叶结点即指树尾端NIL指针或NULL结点）都是黑的。
4、如果一个结点是红的，那么它的两个儿子都是黑的。
5、对于任意结点而言，其到叶结点树尾端NIL指针的每条路径都包含相同数目的黑结点。

红黑树
红黑树 —-图片来自维基百科

按照上述性质我们可以很容易的构造一棵红黑树，但是当在对红黑树进行插入和删除等操作时，对树做了修改可能会破坏红黑树的性质。为了继续保持红黑树的性质，可以通过对结点进行重新着色，以及对树进行相关的旋转操作，即通过修改树中某些结点的颜色及指针结构，来达到对红黑树进行插入或删除结点等操作后继续保持它的性质或平衡的目的。这里有三个比较重要的操作，左旋、右旋和着色，着色比较好理解，黑色或者红色，我们重点看一下左旋和右旋。
左旋

左旋
左旋

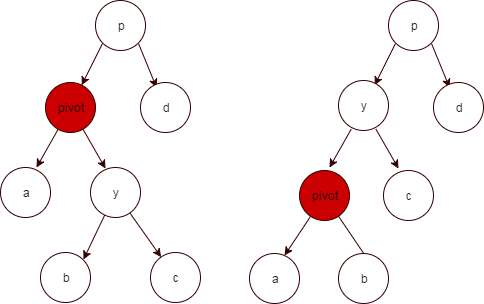
如上图所示，当需要将pivot节点左旋时，我们假设它的右孩子y不是NIL[T]，pivot可以为任何不是NIL[T]的左子结点。左旋以pivot到y之间的链为“支轴”进行，它使y成为该子树的新根，而y的左孩子b则成为pivot的右孩子。

右旋

右旋
右旋

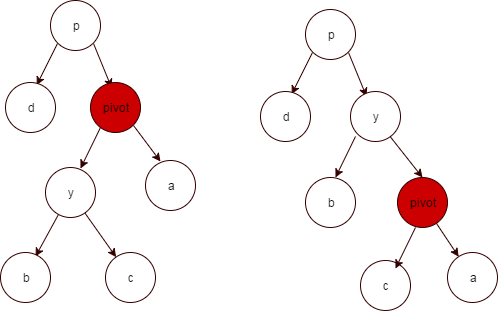
如上图所示，当需要将pivot节点右旋时，我们假设它的左孩子y不是NIL[T]，pivot可以为任何不是NIL[T]的右子结点。右旋以pivot到y之间的链为“支轴”进行，它使y成为该子树的新根，而y的左孩子b则成为pivot的右孩子。

关于红黑树就说到这里，感兴趣的同学可以看一下July大神的博文教你初步了解红黑树，下面我们结合源码来看一下TreeMap是怎么样利用这一结构实现的。

几个基本属性

1
2
3
4
5
6
7
8
9
10
11
12
13
14
private final Comparator<? super K> comparator;//比较器
private transient Entry<K,V> root; //根节点
/**
 * The number of entries in the tree
 */
private transient int size = 0;//元素数量
/**
 * The number of structural modifications to the tree.
 */
private transient int modCount = 0;//修改记录

通过以上代码我们可以看到，TreeMap内部维护着一个比较器comparator，通过这个比较器，可以实现根据key的排序。root是TreeMap存储元素的根节点，这个根节点的类型为Entry<K,V>，是基于红黑树实现的一个数据结构，下面是部分源码，我们可以看到这个Entry<K,V>直接继承了Map.Entry<K,V>，除了基本的key和vlaue属性，还多了其他属性。left表示红黑树结构的左子树节点的引用，right表示右子树几点的引用，parent表示父节点的引用，还有一个color表示当前节点的颜色，这是一个布尔类型的值，通过设置true或者false来表示黑色或者红色。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
static final class Entry<K,V> implements Map.Entry<K,V> {
    K key;//存储键
    V value;//存储值
    Entry<K,V> left;//左子树节点引用
    Entry<K,V> right;//右子树节点引用
    Entry<K,V> parent;//父节点引用
    boolean color = BLACK;//颜色
    /**
     * Make a new cell with given key, value, and parent, and with
     * {@code null} child links, and BLACK color.
     */
    Entry(K key, V value, Entry<K,V> parent) {
        this.key = key;
        this.value = value;
        this.parent = parent;
    }

构造方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
//默认构造方法，comparator为空，代表使用key的自然顺序来维持TreeMap的顺序，这里要求key必须实现Comparable接口
public TreeMap() {
    comparator = null;
}
//根据已有的Map构造TreeMap
public TreeMap(Comparator<? super K> comparator) {
    this.comparator = comparator;
}
//构造一个指定map的TreeMap，同样比较器comparator为空，使用key的自然顺序排序
public TreeMap(Map<? extends K, ? extends V> m) {
    comparator = null;
    putAll(m);
}
//构造一个指定SortedMap的TreeMap，根据SortedMap的比较器来来维持TreeMap的顺序
public TreeMap(SortedMap<K, ? extends V> m) {
    comparator = m.comparator();
    try {
        buildFromSorted(m.size(), m.entrySet().iterator(), null, null);
    } catch (java.io.IOException cannotHappen) {
    } catch (ClassNotFoundException cannotHappen) {
    }
}

TreeMap提供了四个构造方法，默认的无参构造方法实例化一个key的自然序列的顺序，要求key必须实现Comparable接口。同时还提供了一个指定比较器的构造方法，用以使用指定比较器实现排序。

添加元素

将一个节点添加到红黑树中，通常需要下面几个步骤：

1、将红黑树当成普通二叉查找树，将节点插入。
2、将新插入的节点设置为红色。
3、通过旋转和着色，使它恢复平衡，重新变成一颗符合规则的红黑树。

下面我们重点看一下添加元素的实现方式：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
public V put(K key, V value) {
    Entry<K,V> t = root;
    if (t == null) {//如果root为null 说明是添加第一个元素 直接实例化一个Entry 赋值给root
        compare(key, key); // type (and possibly null) check
        root = new Entry<>(key, value, null);
        size = 1;
        modCount++;
        return null;
    }
    int cmp;
    Entry<K,V> parent;//如果root不为null，说明已存在元素 
    // split comparator and comparable paths
    Comparator<? super K> cpr = comparator; 
    if (cpr != null) { //如果比较器不为null 则使用比较器
        //找到元素的插入位置
        do {
            parent = t; //parent赋值
            cmp = cpr.compare(key, t.key);
            //当前key小于节点key 向左子树查找
            if (cmp < 0)
                t = t.left;
            else if (cmp > 0)//当前key大于节点key 向右子树查找
                t = t.right;
            else //相等的情况下 直接更新节点值
                return t.setValue(value);
        } while (t != null);
    }
    else { //如果比较器为null 则使用默认比较器
        if (key == null)//如果key为null  则抛出异常
            throw new NullPointerException();
        @SuppressWarnings("unchecked")
            Comparable<? super K> k = (Comparable<? super K>) key;
       
        //找到元素的插入位置
        do {
            parent = t;
            cmp = k.compareTo(t.key);
            if (cmp < 0)
                t = t.left;
            else if (cmp > 0)
                t = t.right;
            else
                return t.setValue(value);
        } while (t != null);
    }
    Entry<K,V> e = new Entry<>(key, value, parent);//定义一个新的节点
    //根据比较结果决定插入到左子树还是右子树
    if (cmp < 0)
        parent.left = e;
    else
        parent.right = e;
    fixAfterInsertion(e);//保持红黑树性质  插入后进行修正
    size++;//元素树自增
    modCount++; 
    return null;
}

fixAfterInsertion方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
 // 新增节点后对红黑树的调整方法 */
private void fixAfterInsertion(Entry<K,V> x) {
    // 将新插入节点的颜色设置为红色
    x. color = RED;
    // while循环，保证新插入节点x不是根节点或者新插入节点x的父节点不是红色（这两种情况不需要调整）
    while (x != null && x != root && x. parent.color == RED) {
        // 如果新插入节点x的父节点是祖父节点的左孩子
        if (parentOf(x) == leftOf(parentOf (parentOf(x)))) {
            // 取得新插入节点x的叔叔节点
            Entry<K,V> y = rightOf(parentOf (parentOf(x)));
            // 如果新插入x的父节点是红色
            if (colorOf(y) == RED) {
                // 将x的父节点设置为黑色
                setColor(parentOf (x), BLACK);
                // 将x的叔叔节点设置为黑色
                setColor(y, BLACK);
                // 将x的祖父节点设置为红色
                setColor(parentOf (parentOf(x)), RED);
                // 将x指向祖父节点，如果x的祖父节点的父节点是红色，按照上面的步奏继续循环
                x = parentOf(parentOf (x));
            } else {
                // 如果新插入x的叔叔节点是黑色或缺少，且x的父节点是祖父节点的右孩子
                if (x == rightOf( parentOf(x))) {
                    // 左旋父节点
                    x = parentOf(x);
                    rotateLeft(x);
                }
                // 如果新插入x的叔叔节点是黑色或缺少，且x的父节点是祖父节点的左孩子
                // 将x的父节点设置为黑色
                setColor(parentOf (x), BLACK);
                // 将x的祖父节点设置为红色
                setColor(parentOf (parentOf(x)), RED);
                // 右旋x的祖父节点
                rotateRight( parentOf(parentOf (x)));
            }
        } else { // 如果新插入节点x的父节点是祖父节点的右孩子，下面的步奏和上面的相似，只不过左旋右旋的区分
            Entry<K,V> y = leftOf(parentOf (parentOf(x)));
            if (colorOf(y) == RED) {
                setColor(parentOf (x), BLACK);
                setColor(y, BLACK);
                setColor(parentOf (parentOf(x)), RED);
                x = parentOf(parentOf (x));
            } else {
                if (x == leftOf( parentOf(x))) {
                    x = parentOf(x);
                    rotateRight(x);
                }
                setColor(parentOf (x), BLACK);
                setColor(parentOf (parentOf(x)), RED);
                rotateLeft( parentOf(parentOf (x)));
            }
        }
    }
    // 最后将根节点设置为黑色
    root.color = BLACK;
}

总结

1、基于红黑树（Red-Black tree）的数据结构实现。该映射根据其键的自然顺序进行排序，或者根据创建映射时提供的 Comparator 进行排序，具体取决于使用的构造方法。
2、不允许插入为Null的key
3、可以插入值为Null的Value
4、若Key重复，则后面插入的直接覆盖原来的Value
5、非线程安全
6、根据key排序，key必须实现Comparable接口，可自定义比较器实现排序。
7、TreeMap使用的数据结构决定了他的插入操作变的比较复杂，需要维护一个红黑树，所以TreeMap不适合用在频繁修改的场景，如果不需要实现有序性，则建议使用HashMap，存取效率要高一些。

参考

http://www.jianshu.com/p/fc5e16b5c674
http://blog.csdn.net/v_july_v/article/details/6105630
https://zh.wikipedia.org/wiki/AVL%E6%A0%91
https://zh.wikipedia.org/wiki/%E7%BA%A2%E9%BB%91%E6%A0%91